L'exponentiation rapide en détails

Si vous avez fait une prépa ou que vous êtes développeur, vous avez certainement entendu parler de cette méthode pour calculer rapidement des puissances. L'idée sous-jacente est très simple, mais quand je m'y suis intéressé pour la première fois j'ai trouvé que la documentation existante sur internet n'était pas forcément très claire ou exhaustive, que ce soit en anglais ou en français. Il existe de nombreuses implémentations différentes, et certaines sont moins intuitives (mais beaucoup plus amusantes !) que d'autres.

En particulier, certains sites (par exemple l'excellent CP-Algorithms ou même la page Wikipédia en français) présentent une intuition itérative puis une implémentation récursive. D'autres présentent des implémentations dites "de droite à gauche" puis "de gauche à droite" sans expliquer que ces deux versions ne découlent pas simplement l'une de l'autre.

😕

La page Wikipédia anglaise a même un bandeau demandant de l'aide pour clarifier la section qui décrit l'algorithme...

Nous verrons ensemble l'intuition derrière l'exponentiation rapide, puis les différentes implémentations possibles, et la logique sous-jacente pour chacune d'entre elles.

Accrochez-vous, c'est parti ! 🚀

Le problème

Il est fréquent en informatique de devoir calculer des expressions du type $ x^n $. Cette opération est utilisée en cryptographie, en théorie des graphes, et dans bien d'autres domaines.

La méthode naïve consiste à multiplier "bêtement" $x$ par lui-même $n$ fois:

$$ x^n = x \times x \times ... \times x $$

On aura alors effectué $n-1$ opérations : cette méthode est d'une complexité $O(n)$ : elle est donc gourmande en opérations si $n$ est très grand. En fait, il est possible de calculer $x^n$ avec une complexité $O(log(n))$ !

L'intuition

Prenons pour exemple le calcul de $3^{13}$.

La méthode naïve donne le résultat en 12 multiplications :

$$ 3^{13} = 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 $$

Comme $x^{m+n} = x^m \times x^n $, on peut aussi écrire :

$$ 3^{13} = 3^8 \times 3^4 \times 3 $$

Or, comme $(x^{m})^{n} = x^{m \times n} $, on a :

$$ \begin{align*} 3^4 = (3^2)^2 \\ 3^8 = (3^4)^2 \end{align*} $$

De sorte que si l'on effectue ces opérations :

\begin{align*} 3 \times 3 &= 3^{2} \\ 3^2 \times 3^2 &= 3^4 \\ 3^4 \times 3^4&= 3^8 \\ 3^8 \times 3^4 \times 3 &= 3^{13} \end{align*}

On a calculé $3^{13}$ en seulement 5 multiplications !

L'exponentiation rapide, c'est simplement calculer en utilisant une décomposition maligne en carrés successifs !

Le point de vue binaire

En fait, on peut toujours trouver une telle décomposition en carrés successifs : il suffit d'écrire l'exposant $n$ en base 2 et de prendre les puissances correspondant aux bits valant 1.

Exemple : 13 s'écrit $\underset{8}{1} \underset{4}{1} \underset{2}{0}\underset{1}{1} $, et on a bien $ 3^{13} = 3^8 \times 3^4 \times 3^1$

Comme la notation binaire de $n$ comporte exactement $ \lfloor log(n) \rfloor + 1$ chiffres, on fait :

$ \lfloor log(n) \rfloor $ multiplications pour calculer les carrés successifs
$ \lfloor log(n) \rfloor $ multiplications ou moins (bits à 0) pour les multiplier entre eux et obtenir le résultat

💡

Le nombre de bits à 1 dans la représentation binaire de $n$ est appelé poids de Hamming de $n$. Cette notion est même plus large : elle définit, pour toute chaîne de caractères, le nombre d'éléments différents de l'élément nul dans la chaîne.

L'exponentiation rapide permet donc de calculer $ x^n $ en maximum $ 2 \lfloor log(n) \rfloor $ opérations c'est à dire en $O(log(n))$. C'est donc nettement plus rapide, et toutes les fonctions de calcul de puissances disponibles dans les librairies standards (e.g. math.pow en Python) implémentent cette idée !

Implémentations

A partir du point de vue binaire (de droite à gauche)

L'implémentation la plus simple (à mon sens) de l'exponentiation rapide consiste à traduire la méthode vue ci-dessus directement. En Python :

def fast_pow(x, n):
    next_power = x
    result = 1
    binary_decomposition = bin(n) # Returns the binary notation of n in a string (e.g. 0b100101)
    for i in binary_decomposition[:1:-1]: # Strip the 0b prefix and read bits from right to left
        if int(i) == 1:
            result = result*next_power
        next_power = next_power*next_power
    return result

Avec cette méthode, on parcourt les bits de l'exposant de droite à gauche.

Avec la méthode de Hörner (de gauche à droite)

Il est également possible de calculer l'exponentiation rapide en parcourant les bits de gauche à droite. Cette façon de faire est beaucoup moins naturelle, mais elle est souvent présentée en premier dans les cours de maths ou d'informatique. Il est donc intéressant de la comprendre !

💡

Les anglophones appellent cette méthode "The Square and Multiply method" et utilisent d'ailleurs souvent ce nom pour parler d'exponentiation rapide en général.

La méthode de Hörner
La méthode de Hörner est une méthode pour évaluer un polynôme avec le moins d'opérations possibles (tiens, tiens, ça vous rappelle quelque chose ?).

Prenons par exemple le polynôme $p(x) = 3x^4 - 2x^3 + x^2 - x + 3$. La méthode naïve pour l'évaluer en $x_0$ consisterait à d'abord calculer $x_0^4$ puis $x_0^3$, $x_0^2$ et ainsi de suite, puis de multiplier chaque puissance par son coefficient et de sommer les termes obtenus. On peut montrer que pour un polynôme de degré $n$ il faudrait $ \frac{n(n+1)}{2}$multiplications et $n-1$ additions, soit une complexité en $O(n^2)$.

L'idée d'Hörner, c'est de factoriser le polynôme au maximum avant de l'évaluer.

\begin{align*} p(x) &= 3x^4 - 2x^3 + x^2 - x + 3 \\ &= x(x(x(3x - 2) + 1) - 1) + 3 \end{align*}

Si l'on évalue le polynôme sous cette deuxième forme, en commençant par le terme au centre des parenthèses, on n'a plus que $n$ multiplications à faire !

Il n'est d'ailleurs même pas nécessaire d'écrire le polynôme sous cette forme : la liste des coefficients suffit, puisqu'ils sont conservés.

Pour tout polynôme $ P(x) = \sum_{i=0}^{n} a_{i}x^{i} $, on peut calculer $ P(x_{0}) $ avec l'algorithme suivant:

\begin{align*} &\;r \leftarrow a_{n} \\ &\text{for i in (n-1)\dots0 do} \\ &\;\;\; r \leftarrow x_{0}r + a_{i} \\ &\text{done} \end{align*}

On part ainsi du coefficient le plus à gauche, et on avance vers la droite.

Retour à nos moutons
Très bien, me direz-vous, mais quel est le rapport ? 🤔
Reprenons notre calcul de $ x^n $ (c'est tout de même pour ça que vous êtes là). Si $n$ s'écrit $b_{i}b_{i-1}...b_{0}$ en binaire, alors on remarque que $ n $ est la valeur du polynôme suivant en 2 :

$$ P(x) = b_{i}x^{i} + b_{i-1}x^{i-1} + ... + b_{0}$$

Si l'on applique la méthode de Hörner pour obtenir un algorithme pour calculer $x^{n}$, on obtient ceci :

\begin{align*} &\;r \leftarrow x \\ &\text{for i in (n-1)\dots0 do}\\ &\;\;\; r \leftarrow r^{2}*x^{b_{i}} \\ &\text{done} \\ &\text{return r} \end{align*}

Qui se traduit en Python comme suit :

def fast_pow_left_to_right(x, n):
    result = x
    binary_decomposition = bin(n) # Returns the binary notation of n in a binary string (e.g. 0b100101)
    for i in binary_decomposition[2:]: # Strip the 0b prefix and read bits from left to right
        result = result*result
        if int(i) == 1:
            result = result*x
    return result

On voit bien pourquoi cette méthode est dite de gauche à droite, ou square and multiply. A l'inverse de la précédente, qui était de droite à gauche, et serait plutôt multiply and square !

Avec une autre façon de lire des nombres binaires (de droite à gauche, toujours)

Maintenant que je vous ai fait découvrir (peut-être !) la règle de Hörner et une façon de construire l'algorithme de gauche à droite, je me dois de vous montrer une autre façon de le retrouver, beaucoup plus simple !

🤭

Eh oui, je vous ai bien eu... Désolé !

Si vous êtes comme moi, vous avez probablement l'habitude de faire vos conversions binaire - décimal en partant de la droite et en ajoutant les puissances successives de 2 comme suit :

$$ 1011_{2} = 1 + 2 + 8 = 13_{10}$$

Mais il existe une autre façon de faire cette conversion, en appliquant la méthode suivante :

On lit la représentation binaire de gauche à droite
On part de 1
A chaque fois qu'on avance d'un cran vers la gauche, on multiplie le résultat par 2
Si le bit vaut 1, on ajoute 1

Ainsi, pour l'exemple précédant, en repartant de $ 1011_{2} $:

\begin{align*} &1: r = 1 \\ &1: r = 2*r + 1 = 3 \\ &0: r = 2*r = 6 \\ &1: r = 2*r +1 = 13 \end{align*}

Quand on "passe à la puissance", multiplier par 2 devient mettre au carré, et ajouter 1 devient multiplier par la base. On retombe alors immédiatement sur l'algorithme de gauche à droite précédent ! C'est-y pas génial ? 🤩

Récursive

Une dernière, et après je vous laisse tranquille, promis !

Celle-ci est rapide, il suffit de remarquer que :

\[ x^{n} = \begin{cases} (x^{\frac{n}{2}})^{2} &\text{si n est pair} \\ (x^{\frac{n-1}{2}})^{2}*x &\text{si n est impair} \end{cases} \]

D'où l'on déduit immédiatement l'algorithme récursif suivant :

def fast_pow_recursive(x, n):
    if n == 0:
        return 1
    p = fast_pow_recursive(x, n//2)
    if n % 2 == 0:
        return p*p
    else:
        return x * p * p

Résumé

Boooon, vous avez bien mérité un petit schéma pour résumer tout ça ! 😃

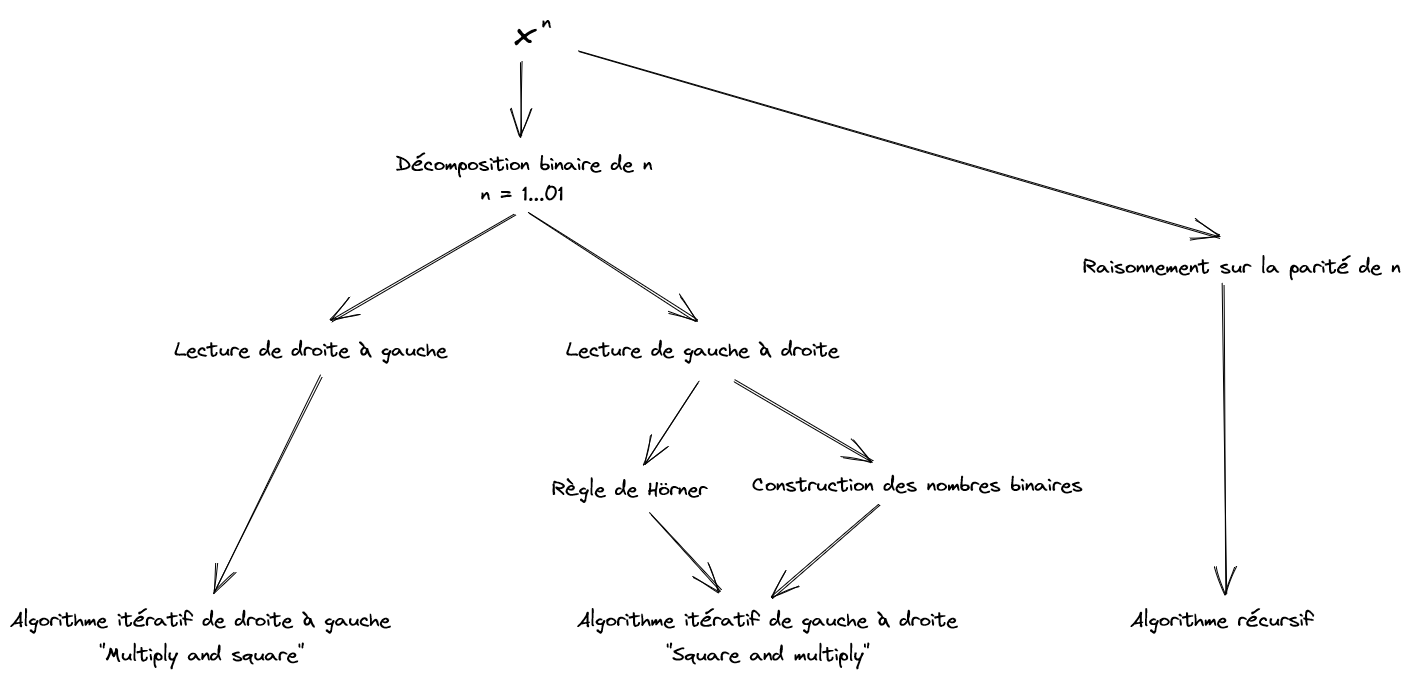
Quelle méthode faut-il utiliser ?

Eh bien... à vrai dire, aucune. Tout simplement parce que quel que soit le langage que vous utilisez, la librairie standard fournit certainement une fonction très optimisée pour calculer des puissances !

Il existe d'ailleurs des versions plus poussées des algorithmes présentés ci-dessus. L'une d'entre-elles, appelée exponentiation rapide à arité k (k-arity rapid exponentiation en anglais, rien à voir avec le beurre), permet de faire le calcul en groupant les bits.

Python utilise l'algorithme de gauche à droite si l'exposant comporte moins de 8 chiffres et l'algorithme d'arité 5 sinon (source).

Pourquoi des carrés et non des cubes ?

Il reste un dernier point à éclaircir. S'il est si efficace d'utiliser des carrés successifs pour calculer une exponentiation, pourquoi ne pas utiliser des cubes ? Après tout, 3 c'est mieux que 2... non ?

Eh bien non ! Car même si en effet, "3 c'est mieux que 2", il faut deux multiplications pour calculer $x^3$ contre seulement une pour $x^2$ ! Ainsi:

Avec des carrés, deux multiplications permettent de passer de $x^i$ à $x^{4i}$
Avec des cubes, deux multiplication ne font passer que de $x^i$ à $x^{3i}$

Il est donc bien plus efficace d'utiliser des carrés que des cubes... en revanche on peut utiliser des puissances de deux (4, 8, etc), ce qui revient à l'algorithme k-ary évoqué plus haut !

Conclusion

J'espère que ce petit tour d'horizon de l'exponentiation binaire vous a plu ! Il est, certes, de peu d'intérêt pratique, mais je trouve fascinant de voir comment une idée en apparence simple peut être déclinée de différentes façons pour aboutir à des algorithmes différents mais accomplissant la même chose !

C'était également mon premier blog post. Promis, le prochain sera moins long !

A la prochaine ! 👋